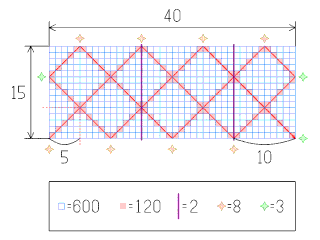
 40と15に関する次の要素が埋め込まれた図: 積(600)、 商と剰余(40÷15=2余り10)、 最小公倍数(120)、 最大公約数(5)、 比(8:3)
40と15に関する次の要素が埋め込まれた図: 積(600)、 商と剰余(40÷15=2余り10)、 最小公倍数(120)、 最大公約数(5)、 比(8:3)  幾何学的に2つの整数(WとH)及びその最大公約数並びに最小公倍数を長さとして表せる。この図では、WとHを長方形の幅と高さに割り当て、最大公約数をユークリッドの互除法に基づく方法で長さとして求めだし、長方形の面積(WとHの積)を最大公約数で割った結果として最小公倍数も長さとして求めだしている。
幾何学的に2つの整数(WとH)及びその最大公約数並びに最小公倍数を長さとして表せる。この図では、WとHを長方形の幅と高さに割り当て、最大公約数をユークリッドの互除法に基づく方法で長さとして求めだし、長方形の面積(WとHの積)を最大公約数で割った結果として最小公倍数も長さとして求めだしている。 最小公倍数(さいしょうこうばいすう、英: least common multiple)とは、 ではない複数の整数の公倍数のうち最小の自然数を指す。度々、L.C.M.やlcm等の省略形で記述される。
ではない複数の整数の公倍数のうち最小の自然数を指す。度々、L.C.M.やlcm等の省略形で記述される。
定義
2つ以上の整数  の最小公倍数とは、
の最小公倍数とは、 の公倍数のうち最小の正整数である。
の公倍数のうち最小の正整数である。
つまり、 を、素数 (prime) p を用いて
を、素数 (prime) p を用いて

と素因数分解したとき、 の最小公倍数は
の最小公倍数は

で与えられる。
例えば、12 と 16 の最小公倍数は 48 である。
- 12 = 22×31
- 16 = 24
- 48 = 24×31
諸概念
公倍数は最小公倍数の倍数である。
証明
 の最小公倍数を
の最小公倍数を  とする.
とする.  の一般の公倍数を
の一般の公倍数を  とし,
とし, と置く。 変形して
と置く。 変形して  …① ①右辺は
…① ①右辺は  は
は  の公倍数、
の公倍数、 も同じく
も同じく  の公倍数。 よって①の左辺
の公倍数。 よって①の左辺  は
は  の公倍数になる。 しかし
の公倍数になる。 しかし となり、最小公倍数
となり、最小公倍数  よりも一般公倍数
よりも一般公倍数  が小さく矛盾. すなわち
が小さく矛盾. すなわち  。よって公倍数
。よって公倍数  であり最小公倍数の倍数となっている.(証明終)
であり最小公倍数の倍数となっている.(証明終)
正整数 に対して、
に対して、 と
と の最大公約数
の最大公約数 と最小公倍数
と最小公倍数 との間には
との間には

という関係がある。
しかし、この関係式は3つ以上の正整数に対しては一般には成立しない。例えば、 とすると、
とすると、 であるが、
であるが、 である。
である。
多項式の最小公倍数
多項式の でない公倍数のうち、最も次数の低いものを最小公倍数という。例えば、
でない公倍数のうち、最も次数の低いものを最小公倍数という。例えば、 と
と の最小公倍数は
の最小公倍数は である。
である。
多項式の最小公倍数は定数倍を除いて1つしか存在しない。
参考文献
- 高木貞治『初等整数論講義第2版』共立出版、東京、1971年。
関連項目



































