Heavisideova funkce

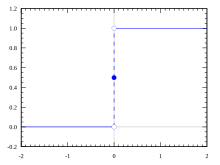
Heavisideova funkce (také jednotkový skok) je nespojitá funkce, jejíž hodnota je nulová pro zápornou hodnotu argumentu a rovna jedné pro kladnou hodnotu argumentu. Hodnota funkce pro nulový argument není podstatná a proto je různými autory definována odlišně (viz níže).

Často se používá v teorii řízení a při zpracování signálu, kde slouží k reprezentaci jednorázové změny signálu. Pojmenována byla po anglickém učenci Oliveru Heavisideovi.

Definice

Heavisidova funkce (s parametrem p) se definuje předpisem:

${\displaystyle H_{p}(x)=\left\{{\begin{matrix}0&{\mbox{ pro }}x<0\\p&{\mbox{ pro }}x=0\\1&{\mbox{ pro }}x>0\end{matrix}}\right.}$,

kde 0 ≤ p ≤ 1 je reálné číslo určující hodnotu funkce v bodě 0 (platí ${\displaystyle p=H_{p}(0)}$).

Index p je většinou volen pevně a v zápise se vynechává. Heavisidova funkce se potom značí pouze H(x).

Hodnota v nule

Parametr ${\displaystyle p}$ z definice funkce se nejčastěji volí jako 0, 1/2 nebo 1. Pro hodnotu 1/2 svědčí symetrie výsledné funkce a fakt, že hodnota zpětné transformace Fourierova obrazu funkce v bodech nespojitosti je aritmetický průměr limit zleva a zprava. Důvodem jiné volby může být praktičnost při jistých způsobech použití. V mnoha případech na hodnotě v nule vůbec nezáleží, např. integrujeme-li složený výraz s touto funkcí, neboť Lebesgueova míra množiny ${\displaystyle \{0\}}$ je nulová.

Nastavíme-li ${\displaystyle p=H(0)=1/2}$, můžeme definovat funkci pomocí znaménkové funkce (signum):

${\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}}$

Pro případ, kdy ${\displaystyle p=1}$ nebo ${\displaystyle p=0}$ můžeme též chápat Heavisideovu funkci takto: ${\displaystyle H_{1}=\chi _{\langle 0,\infty )}}$ respektive ${\displaystyle H_{0}=\chi _{(0,\infty )}}$ kde ${\displaystyle \chi _{M}}$ značí charakteristickou funkci množiny ${\displaystyle M}$.

Vlastnosti

Mezi jednotkovým skokem a Diracovou funkcí existuje vztah, který lze zapsat jako

${\displaystyle H(x)=\int _{-\infty }^{x}\delta (t)\mathrm {d} t}$

Derivací Heavisideovy funkce je tedy Diracova delta funkce, primitivní funkcí je tzv. náběhová funkce.

Odkazy

Související články

• Charakteristická funkce
• Diracovo delta
• Macaulayova závorka
• Náběhová funkce

Externí odkazy

• Obrázky, zvuky či videa k tématu Heavisideova funkce na Wikimedia Commons
• (anglicky) MathWorld, Heaviside Step Function: http://mathworld.wolfram.com/…
• (anglicky) PlanetMath, Heaviside step function: http://planetmath.org/… Archivováno 2. 2. 2009 na Wayback Machine.
• (anglicky) MathWorks, Heaviside: http://www.mathworks.com/…